Đặt điện áp \(u=U\sqrt{2}\cos \left( \omega t \right)\,\left( V \right)\)
Câu hỏi :
Đặt một điện áp xoay chiều \(u=U\sqrt{2}\cos \left( \omega t \right)\,\left( V \right)\) vào hai đầu mạch điện AB mắc nối tiếp theo thứ tự gồm điện trở R, cuộn dây không thuần cảm (L, r) và tụ điện C với R = r. Gọi N là điểm nằm giữa điện trở R và cuộn dây, M là điểm nằm giữa cuộn dây và tụ điện. Điện áp tức thời \({{u}_{AM}}\) và \({{u}_{NB}}\) vuông pha với nhau và có cùng một giá trị hiệu dụng là \(30\sqrt{5}\,V\). Giá trị của U bằng: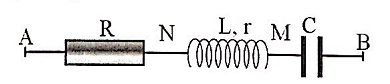
A. \(60\sqrt{2}\,V\)
B. \(120\sqrt{2}\,V\)
C. 60 V.
D. 120 V.
* Đáp án
A
* Hướng dẫn giải
Giản đồ vectơ của mạch:
.png)
Theo đề bài ta có:
\(\left\{ \begin{align} & {{U}_{NB}}={{U}_{AM}}\Rightarrow NB=AM \\ & \angle AMH=\angle BNH \\ \end{align} \right.\Rightarrow \Delta AHM=\Delta BHN\)
( cạnh huyền và góc nhọn bằng nhau)
Suy ra :
\({{U}_{R}}={{U}_{r}}={{U}_{L}}=x\Rightarrow \left\{ \begin{align} & AH=2x \\ & MH=x \\ \end{align} \right.\Rightarrow AM={{U}_{AM}}=\sqrt{{{\left( 2x \right)}^{2}}+{{x}^{2}}}\)
Ta lại có:
\({{U}_{AM}}=30\sqrt{5}\Rightarrow \sqrt{{{\left( 2x \right)}^{2}}+{{x}^{2}}}=30\sqrt{5}\Rightarrow \left\{ \begin{align} & x=30V \\ & AH=2x=60V \\ \end{align} \right.\)
Mà:
\(\Delta AHM=\Delta BHN\Rightarrow AH=HB=2x=60\)
\(\Rightarrow AB=AH\sqrt{2}=60\sqrt{2}\left( V \right)\Rightarrow U=60\sqrt{2}\left( V \right)\)
Câu hỏi trên thuộc đề trắc nghiệm dưới đây !
Đề thi thử THPT QG năm 2021 môn Vật Lý Trường THPT Lạng Giang
Copyright © 2021 HOCTAP247
