Từ một tấm tôn có hình dạng elip với độ dài trục lớn bằng độ dài trục bé bằng . Người thợ cần cắt một tấm tôn có dạng hình chữ nhật nội tiếp elíp, sau đó gò tấm tôn hình chữ nhật n...
Câu hỏi :
Từ một tấm tôn có hình dạng elip với độ dài trục lớn bằng 6 độ dài trục bé bằng 4. Người thợ cần cắt một tấm tôn có dạng hình chữ nhật nội tiếp elíp, sau đó gò tấm tôn hình chữ nhật này thành một hình trụ không có đáy (như hình bên).Tính thể tích lớn nhất có thể thu được của khối trụ đó?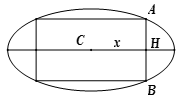
.png)
A. \(V = \frac{{4\sqrt 3 }}{\pi }\)
B. \(V = \frac{{3\sqrt 2 }}{\pi }\)
C. \(V = \frac{{5\sqrt 2 }}{\pi }\)
D. \(V = \frac{{8\sqrt 3 }}{\pi }\)
* Đáp án
D
* Hướng dẫn giải
Ta có phương trình đường \(\left( E \right):\frac{{{x}^{2}}}{9}+\frac{{{y}^{2}}}{4}=1\Rightarrow y=\frac{2}{3}\sqrt{9-{{x}^{2}}}\).
Gọi bán kính đáy hình trụ là r, đường cao là h
Chu vi một đáy của hình trụ là: \(2\pi r=2x\Leftrightarrow r=\frac{x}{\pi }\)
\(AH=\frac{2}{3}\sqrt{9-{{x}^{2}}}\Rightarrow h=2AH=\frac{4}{3}\sqrt{9-{{x}^{2}}}\)
\({{V}_{tru}}=\pi .{{r}^{2}}.h=\pi {{\left( \frac{x}{\pi } \right)}^{2}}.\frac{4}{3}\sqrt{9-{{x}^{2}}}=\frac{4}{3\pi }{{x}^{2}}\sqrt{9-{{x}^{2}}}\)
Đặt \(f\left( x \right)=\frac{4}{3\pi }{{x}^{2}}\sqrt{9-{{x}^{2}}}\,\,\,\left( 0<x<3 \right)\)
\(f'\left( x \right) = \frac{4}{{3\pi }}\left[ {\frac{{18x - 3{x^3}}}{{\sqrt {9 - {x^2}} }}} \right] \Rightarrow f'\left( x \right) = 0 \Leftrightarrow \left[ \begin{array}{l} x = 0\,(L)\\ x = \sqrt 6 (N)\\ \,x = - \sqrt 6 \,(L) \end{array} \right.\)
Suy ra \({V_{\max }} = \frac{{8\sqrt 3 }}{\pi } \Leftrightarrow x = \sqrt 6 \)
Câu hỏi trên thuộc đề trắc nghiệm dưới đây !
Đề thi thử THPT QG năm 2021 môn Toán - Trường THPT Thanh Oai B
Copyright © 2021 HOCTAP247
