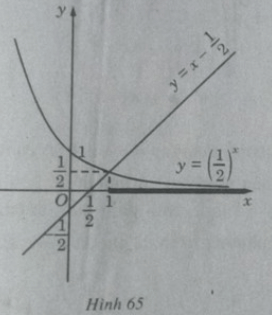Giải các bất phương trình sau bằng đồ thị: a) (1/2)^x < x - 1/2

* Hướng dẫn giải

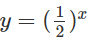
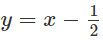
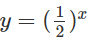
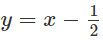
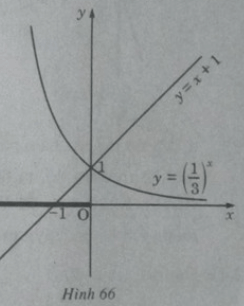
a) Vẽ đồ thị của hàm số  và đường thẳng  trên cùng một hệ trục tọa độ (H.65), ta thấy chúng cắt nhau tại điểm có hoành độ x = 1. Với x > 1 đồ thị của hàm số  nằm phía dưới đường thẳng  . Vậy tập nghiệm của bất phương trình đã cho là (1;+∞)

b) Vẽ đồ thị của hàm số 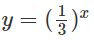 và đường thẳng y = x + 1 trên cùng một hệ trục tọa độ (H.66), ta thấy chúng cắt nhau tại điểm có hoành độ x = 0.

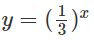
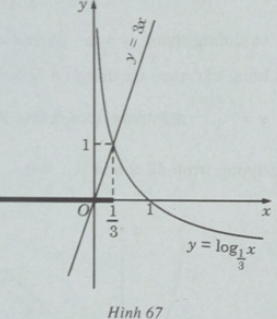
Khi x < 0 đồ thị của hàm số  nằm phía trên đường thẳng y = x + 1. Vậy tập nghiệm của bất phương trình đã cho là (-∞;0]

c) Vẽ đồ thị của hàm số 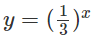 và đường thẳng y = 3x trên cùng một hệ trục tọa độ ta thấy chúng cắt nhau tại điểm có hoành độ x = 1/3 (H.67)

Khi x < 1/3 đồ thị của hàm số 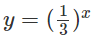 nằm phía trên đường thẳng y = 3x.

Vậy tập nghiệm của bất phương trình đã cho là (-$\infty$;1/3).

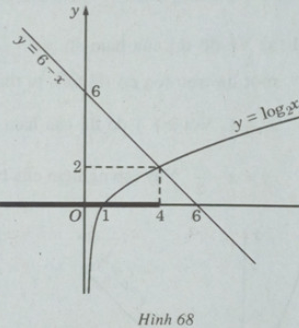
d) Vẽ đồ thị của hàm số y = ${\log }_{2}x$ và đường thẳng y = 6 – x trên cùng một hệ trục tọa độ, ta thấy chúng cắt nhau tại điểm có hoành độ x = 4 (H.68).

Khi x < 4, đồ thị của hàm số y = ${\log }_{2}x$ nằm phía dưới y = 6 – x . Vậy tập nghiệm của bất phương trình đã cho là (-$\infty$;4].