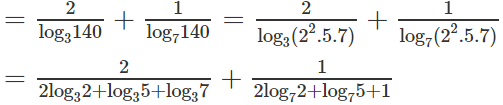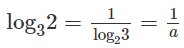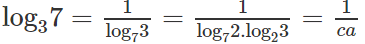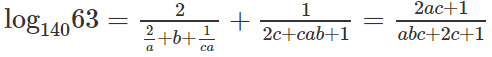Trang chủ
Đề thi & kiểm tra
Lớp 12
Toán học
Giải sbt Giải tích 12 Bài 3: Lôgarit !!
a) Cho a = log 3 của 15, b =...
a) Cho a = log 3 của 15, b = log 3 của 10. Hãy tính log căn 3 của 50 theo a và b
Câu hỏi :
a) Cho a = , b = . Hãy tính theo a và b.
* Đáp án
* Hướng dẫn giải
a) Ta có:
a = = = + = 1 +
Suy ra = a – 1
b = = = +
Suy ra = b − = b − (a − 1) = b – a + 1
Do đó:
= = 2 + 4 = 2 (b – a + 1) + 4(a − 1) = 2a + 2b − 2
b) Ta có:
= = 2 +
Từ đề bài suy ra:
= = cab
Vậy
Câu hỏi trên thuộc đề trắc nghiệm dưới đây !
Giải sbt Giải tích 12 Bài 3: Lôgarit !!
Số câu hỏi: 12
Copyright © 2021 HOCTAP247