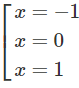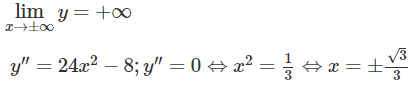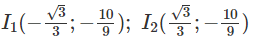Cho hàm số y = 2x^4 − 4x^2 (1) a) Khảo sát sự biến thiên và

* Hướng dẫn giải

a) Tập xác định: D = R

y′=0 ⇔ 

Hàm số đồng biến trên mỗi khoảng (-1; 0) và (1; +$\infty$)

Hàm số nghịch biến trên mỗi khoảng (−$\infty$; −1); (0; 1)

Hàm số đạt cực đại tại x = 0; $y_{CĐ}$ = 0

Hàm số đạt cực tiểu tại x = 1 hoặc x = -1; $y_{CT}$ = −2

Đồ thị có hai điểm uốn:

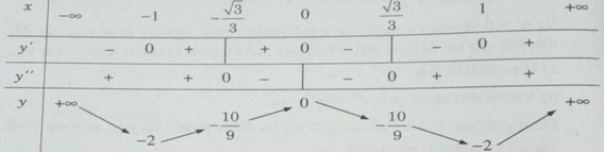
Bảng biến thiên:

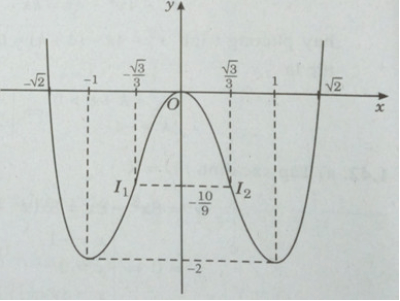
Đồ thị:

Đồ thị cắt trục hoành tại:

b) Ta có: $x^2$|$x^2$ − 2| = m

⇔ 2$x^2$ |$x^2$ − 2| = 2m

⇔|2$x^2$($x^2$ − 2)| = 2m

⇔|2$x^4$ − 4$x^2$| = 2m

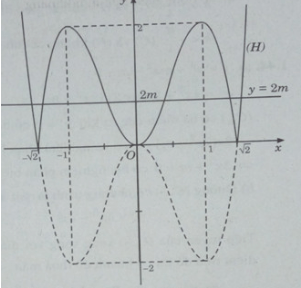
Từ đồ thị hàm số y = 2$x^4$ – 4$x^2$ có thể suy ra đồ thị của hàm số y = |2$x^4$ − 4$x^2$| như sau:

Phương trình: |2$x^4$ − 4$x^2$| = 2m có 6 nghiệm phân biệt khi và chỉ khi đường thẳng y = 2m có 6 nghiệm phân biệt với đồ thị (H)

⇔ 0 < 2m < 2

⇔ 0 < m < 1