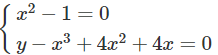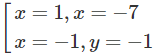Cho hàm số: y = x^3 − (m + 4)x^2 − 4x + m (1) a) Tìm các điểm mà đồ thị của hàm số (1)

* Hướng dẫn giải

a) y = $x^3$ − (m + 4)$x^2$ − 4x + m

⇔ ($x^2$ − 1)m + y − $x^3$ + 4$x^2$ + 4x = 0

Đồ thị của hàm số (1) luôn luôn đi qua điểm A(x; y) với mọi m khi (x; y) là nghiệm của hệ phương trình:

Giải hệ, ta được hai nghiệm:

Vậy đồ thị của hàm số luôn luôn đi qua hai điểm (1; -7) và (-1; -1).

b) y′ = 3$x^2$ − 2(m + 4)x – 4

Δ′ = ${(m+4)}^2$ + 12

Vì Δ’ > 0 với mọi m nên y’ = 0 luôn luôn có hai nghiệm phân biệt (và đổi dấu khi qua hai nghiệm đó). Từ đó suy ra đồ thị của (1) luôn luôn có cực trị.

c) Học sinh tự giải.

d) Với m = 0 ta có: y = $x^3$ – 4$x^2$ – 4x.

Đường thẳng y = kx sẽ cắt (C) tại ba điểm phân biệt nếu phương trình sau có ba nghiệm phân biệt: $x^3$ – 4$x^2$ – 4x = kx.

Hay phương trình $x^2$ – 4x – (4 + k) = 0 có hai nghiệm phân biệt khác 0, tức là: