Cho hàm số f(x)=|x+1|. Khẳng định nào sau đây là sai?

* Hướng dẫn giải

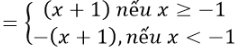
f(-1)=0 ⇒ phương án C đúng

f(x)≥0, ∀x và f(x)=0 ⇔x=-1⇒phương án D đúng

Do đó, hàm số liên tục tại điểm x = -1 

Phương án A đúng

$\underset{x\to -1^{+}}{\lim }\frac{f\left(x\right)-f(-1)}{x-(-1)}=\underset{x\to -1^{+}}{\lim }\frac{x+\text{}1}{x+1}=1$

$\underset{x\to -1^{-}}{\lim }\frac{f\left(x\right)-f(-1)}{x-(-1)}=\underset{x\to -1^{-}}{\lim }\frac{-x-\text{}1}{x+1}=-1$

Suy ra không tồn tại giới hạn của tỉ số

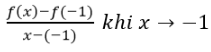
Do đó hàm số đã cho không có đạo hàm tại x=-1.

Vậy chọn đáp án là B