Đặt điện áp \(n = {U_0}{\rm{cos}}\omega t\) vào hai đầu đoạn mạch AB
Câu hỏi :
Đặt điện áp \(n = {U_0}{\rm{cos}}\omega t\) vào hai đầu đoạn mạch AB như hình bên.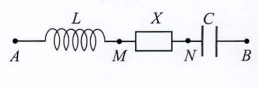
A. 0,25
B. 0,31
C. 0,87
D. 0,71
* Đáp án
C
* Hướng dẫn giải
Ta có:
\(\begin{array}{l}
2LC{\omega ^2} = 1 \Leftrightarrow \frac{{2\omega L}}{{\frac{1}{{\omega C}}}} = 1 \Rightarrow 2{Z_L} = {Z_C}\\
\Rightarrow 2{u_L} = - {u_C} \Rightarrow 2{u_L} + {u_C} = 0\\
\Rightarrow 2{u_{AN}} + {u_{MB}} = 2{u_L} + 2{u_X} + {u_X} + {u_C}\\
\Rightarrow 2{u_{AN}} + {u_{MB}} = 3{u_X}\\
\Rightarrow {u_X} = \frac{{2{u_{AN}} + {u_{MB}}}}{3}
\end{array}\)
Giả sử
\(\begin{array}{l}
{\varphi _{uMB}} = 0 \Rightarrow {\varphi _{uAN}} = \frac{{5\pi }}{{12}}\\
\Rightarrow \left\{ \begin{array}{l}
{u_{MB}} = 90\sqrt 2 \cos \left( {\omega t} \right)\\
{u_{AN}} = 120\sqrt 2 .\cos \left( {\omega t + \frac{{5\pi }}{{12}}} \right)
\end{array} \right.\\
\Rightarrow {u_X} = \frac{{240\sqrt 2 \angle \frac{{5\pi }}{{12}} + 90\sqrt 2 \angle 0}}{3} = 130,7\angle 0,99\\
\Rightarrow {\varphi _{uX}} = 0,99rad
\end{array}\)
Lại có:
\({u_C} = {u_{MB}} - {u_X} = 122,6\angle - 1,1\)
⇒ Độ lệch pha giữa ux và i là:
\({\varphi _X} = {\varphi _{uX}} - {\varphi _i} = 0,99 - 0,47079 = 0,51921rad\)
⇒ Hệ số công suất của X là:
\({x_t} = \left( {k - 0,5} \right)i = \left( {k - 0,5} \right)\frac{{\lambda D}}{a}\)
Câu hỏi trên thuộc đề trắc nghiệm dưới đây !
Đề minh họa kì thi tốt nghiệp THPT môn Vật Lý năm 2021 Bộ GD&ĐT
Copyright © 2021 HOCTAP247
