Một con lắc lò xo treo thẳng đứng, dao động điều hòa tại nơi có g=10m/s2
Câu hỏi :
Một con lắc lò xo treo thẳng đứng, dao động điều hòa tại nơi có g=10m/s2 . Hình bên là đồ thị biểu diễn sự phụ thuộc của độ lớn lực kéo về Fkv tác dụng lên vật và độ lớn lực đàn hồi Fdh của lò xo theo thời gian t .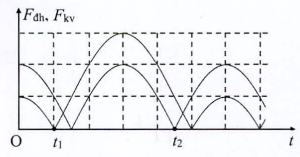
A. 80cm/s
B. 60cm/s
C. 51cm/s
D. 110cm/s .
* Đáp án
B
* Hướng dẫn giải
Giả sử ở vị trí cân bằng, lò xo giãn một đoạn Δl0
Lực đàn hồi và lực phục hồi có độ lớn cực đại là:
\(\left\{ \begin{array}{l}
{F_{dh\max }} = k\left( {\Delta {l_0} + A} \right)\\
{F_{ph\max }} = kA
\end{array} \right. \Rightarrow {F_{dh\max }} > {F_{ph\max }}\)
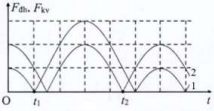
Từ đồ thị ta thấy đồ thị (1) là đồ thị lực phục hồi, đồ thị (2) là đồ thị lực đàn hồi
Ta có:
\(\frac{{{F_{dh\max }}}}{{{F_{ph\max }}}} = \frac{{k\left( {\Delta {l_0} + A} \right)}}{{kA}} = \frac{3}{2} \Rightarrow 2\left( {\Delta {l_0} + A} \right) = 3A \Rightarrow A = 2\Delta {l_0}\)
Nhận xét: lực phục hồi có độ lớn nhỏ nhất tại vị trí cân bằng → tại thời điểm t1, vật ở vị trí cân bằng
Lực đàn hồi có độ lớn nhỏ nhất tại vị trí lò xo không biến dạng → tại thời điểm t2, vật ở vị trí lò xo không biến dạng lần thứ 2 kể từ thời điểm t1
Lực đàn hồi và lực phục hồi có độ lớn cực đại tại vị trí biên dưới → tại thời điểm t3, vật ở vị trí biên dưới lần đầu tiên kể từ thời điểm t2
Ta có vòng tròn lượng giác:

Từ vòng tròn lượng giác ta thấy từ thời điểm t1 đến t2, vecto quay được góc \(\Delta \varphi = \frac{{7\pi }}{6}\left( {rad} \right)\)
Ta có: \(\omega = \frac{{\Delta \varphi }}{{\Delta t}} = \frac{{\frac{{7\pi }}{6}}}{{\frac{{7\pi }}{{120}}}} = 20\left( {rad/s} \right)\)
Lại có:
\(\begin{array}{l}
\omega = \sqrt {\frac{g}{{\Delta l}}} \Rightarrow 20 = \sqrt {\frac{{10}}{{\Delta {l_0}}}} \\
\Rightarrow \Delta {l_0} = 0,025\left( m \right) = 2,5\left( {cm} \right)\\
\Rightarrow A = 5\left( {cm} \right)
\end{array}\)
Khi lò xo giãn 6,5 cm, vật có li độ là:
\(x = \Delta l - \Delta {l_0} = 6,5 - 2,5 = 4\left( {cm} \right)\)
Tốc độ của vật là:
\(v = \omega \sqrt {{A^2} - {x^2}} = 20\sqrt {{5^2} - {4^2}} = 60\left( {cm/s} \right)\)
Câu hỏi trên thuộc đề trắc nghiệm dưới đây !
Đề minh họa kì thi tốt nghiệp THPT môn Vật Lý năm 2021 Bộ GD&ĐT
Copyright © 2021 HOCTAP247
