Cho hình chóp S.ABCD có đáy ABCD là hình thang vuông tại A và B, AB = BC = 1/2AD = 2a. Cạnh bên SA vuông góc với mặt phẳng đáy là SA = 2 căn bậc hai của 2 a. Chứng minh rằng (SBC)...

Câu hỏi :

Cho hình chóp S.ABCD có đáy ABCD là hình thang vuông tại A và B, AB = BC = \(\frac{1}{2}\)AD = 2a. Cạnh bên SA vuông góc với mặt phẳng đáy là SA = \(2\sqrt 2 a.\)

Chứng minh rằng (SBC) ^ (SAB).

* Đáp án

* Hướng dẫn giải

Hướng dẫn giải

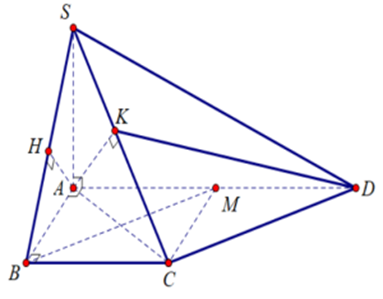
Ta có SA ^ (ABCD) Þ SA ^ BC (1).

Lại có ABCD là hình thang vuông tại B nên AB ^ BC (2).

Từ (1), (2) suy ra BC ^ (SAB) Þ (SBC) ^ (SAB).