Cho tam giác ABC cân tại A, đường trung tuyến AD (D thuộc BC) Gọi E, F thứ tự là trung điểm của AB, AC

Câu hỏi :

Cho tam giác ABC cân tại A, đường trung tuyến $\mathrm{AD}\left(\mathrm{D}\in \mathrm{BC}\right).$ Gọi E, F thứ tự là trung điểm của AB, AC.

a) Chứng minh AEDF là hình bình hành

b) M đối xứng với D qua F. Tứ giác ADCM là hình gì ?

c) Tìm điều kiện của $\mathrm{\Delta ABC}$ để ADCM là hình vuông.

* Đáp án

* Hướng dẫn giải

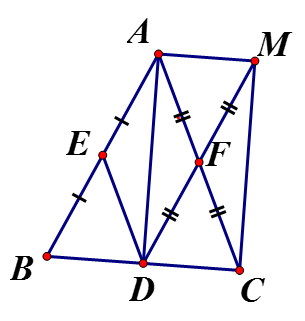
a) Sử dụng đường trung bình ta có ED là đường trung bình $\mathrm{\Delta ABC}\Rightarrow \mathrm{ED}=\frac{1}{2}\mathrm{AC}=\mathrm{AF}$

$\mathrm{ED}//\mathrm{AC}\Rightarrow \mathrm{ED}//\mathrm{AF}\Rightarrow \mathrm{AEDF}$ là hình bình hành

b) Tứ giác ADCM có hai đường chéo cắt nhau tại trung điểm F mỗi đường nên AMCD là hình bình hành và $\mathrm{AD}\perp \mathrm{BC}$ (do $\mathrm{\Delta ABC}$ cân AD đường trung tuyến cũng là đường cao) $\Rightarrow \widehat{\mathrm{ADC}}={90}^0\Rightarrow \mathrm{ADCM}$ là hình chữ nhật

c) ADCM là hình vuông <=> AC là phân giác $\Rightarrow \widehat{\mathrm{MAC}}=\widehat{\mathrm{CAD}}=\widehat{\mathrm{DAB}}={45}^0$

$\Rightarrow \widehat{\mathrm{CAD}}+\widehat{\mathrm{DAB}}=\widehat{\mathrm{CAB}}={45}^0+{45}^0={90}^0\Rightarrow \mathrm{\Delta ABC}$ vuông cân tại A

Vậy $\mathrm{\Delta ABC}$ vuông cân tại A thì AMCD là hình vuông