Cho khối lăng trụ ABC.A'B'C'. Gọi M, N lần lượt là trung điểm

Câu hỏi :

Cho khối lăng trụ \[ABC.A'B'C'\]. Gọi M, N lần lượt là trung điểm của các cạnh \[BB'\], \[CC'\]. Mặt phẳng \[\left( {A'MN} \right)\] chia khối lăng trụ thành hai phần, đặt \[{V_1}\] là thể tích của phần đa diện chứa điểm B và \[{V_2}\] là thể tích của phần còn lại. Tính tỉ số \[\frac{{{V_1}}}{{{V_2}}}\].

* Đáp án

B

* Hướng dẫn giải

Đáp án B

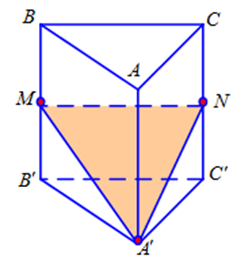
Ta có \({V_2} = {V_{A'.MNC'B'}} = 2{V_{A'.MB'C'}} = 2{V_{M.A'B'C'}}\)

\( = 2.\frac{1}{2}{V_{B.A'B'C'}} = \frac{1}{3}{V_{ABC.A'B'C'}}\)

\( \Rightarrow {V_1} = {V_{ABC.A'B'C'}} - \frac{1}{3}{V_{ABC.A'B'C'}} = \frac{2}{3}{V_{ABC.A'B'C'}} \Rightarrow \frac{{{V_1}}}{{{V_2}}} = 2.\)