Cho hàm số bậc ba y=f(x) có đồ thị (C) như hình vẽ, đường thẳng d có phương
Câu hỏi :
Cho hàm số bậc ba có đồ thị (C) như hình vẽ, đường thẳng d có phương trình Biết phương trình có ba nghiệm . Giá trị của bằng
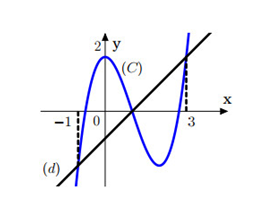
Cho hàm số bậc ba có đồ thị (C) như hình vẽ, đường thẳng d có phương trình Biết phương trình có ba nghiệm . Giá trị của bằng

* Đáp án
A
* Hướng dẫn giải
Chọn A
Phương pháp giải:
Gọi hàm số cần tìm là
Xác định các điểm thuộc đồ thị hàm số rồi thay tọa độ vào hàm số để được hệ bốn ẩn
Giải hệ ta tìm được a; b c; d. Từ đó tìm nghiệm phương trình .
Giải chi tiết:
Gọi hàm số cần tìm là
Từ đồ thị hàm số ta thấy đồ thị (C) cắt đường thẳng d tại ba điểm có hoành độ
Với hay điểm thuộc đồ thị (C)
Với hay điểm (3;2) thuộc đồ thị (C)
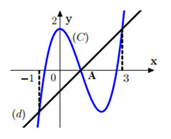
Lại thấy giao điểm của đồ thị (C), trục hoành và đường thẳng là suy ra
Vậy điểm A(0;1) thuộc đồ thị (C).
Thấy đồ thị (C) cắt trục tung tại
Các điểm ; (3;2); (0;1) đều thuộc đồ thị (C) nên ta có hệ phương trình
Suy ra
Phương trình
Suy ra
Câu hỏi trên thuộc đề trắc nghiệm dưới đây !
Bộ 15 đề thi Đánh giá năng lực trường ĐHQG HCM có đáp án !!
Copyright © 2021 HOCTAP247
