Trang chủ
Đề thi & kiểm tra
Lớp 9
Toán học
Đề thi chính thức vào 10 môn Toán Sở GD&ĐT Long An 2016 2017 (có lời giải chi tiết)
Cho tam giác nhọn ABC có AB = AC. Đường...
Cho tam giác nhọn ABC có AB = AC. Đường tròn tâm (O) đường kính AB = 2R cắt cạnh BC, AC lần lượt tại I và K. Tiếp tuyến của đường tròn (O) tại B cắt AI tại D; H là giao điểm của AI...
Câu hỏi :
Cho tam giác nhọn ABC có AB = AC. Đường tròn tâm (O) đường kính AB = 2R cắt cạnh BC, AC lần lượt tại I và K. Tiếp tuyến của đường tròn (O) tại B cắt AI tại D; H là giao điểm của AI và BK a/ Chứng minh tứ giác IHKC là tứ giác nội tiếp được trong đường tròn. b/ Chứng minh BC là tia phân giác của góc DBH. c/ Tính diện tích hình tròn ngoại tiếp tứ giác IHKC theo R trong trường hợp tam giác ABC đều.
A 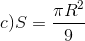
B 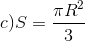
C 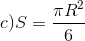
D 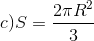
* Đáp án
B
* Hướng dẫn giải
Phương pháp giải:
Câu hỏi trên thuộc đề trắc nghiệm dưới đây !
Đề thi chính thức vào 10 môn Toán Sở GD&ĐT Long An 2016 2017 (có lời giải chi tiết)
Số câu hỏi: 2
Copyright © 2021 HOCTAP247
